Program Linear

Penyelesaian Program Linear

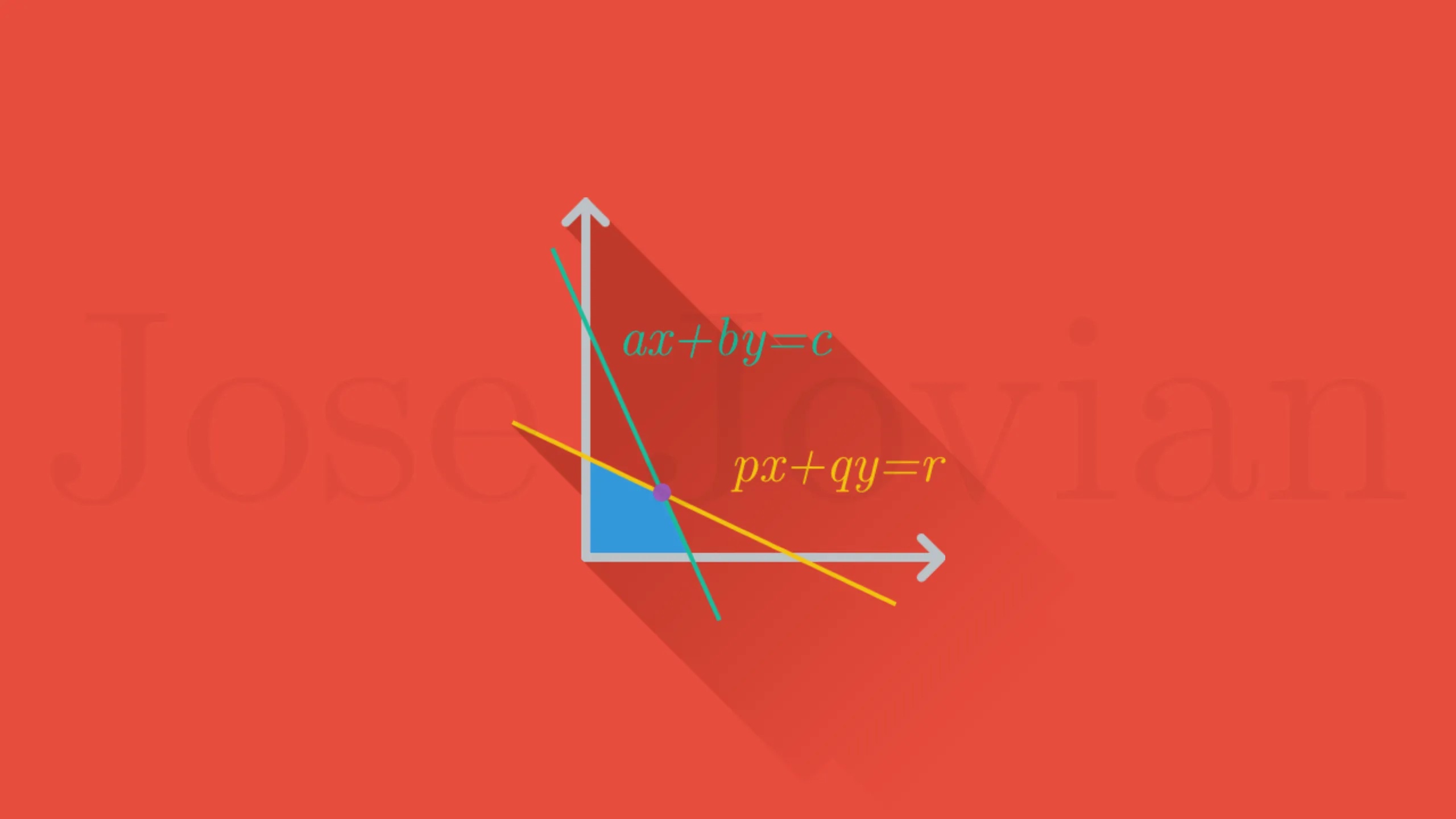
Untuk memudahkan dalam menyelesaikan program linear, metode tabel dapat digunakan untuk mempermudah merancang pertidaksamaan.

Titik yang akan diuji kedalam fungsi objektif ada tiga, salah satunya merupakan titik potong antara dua garis, dan keduanya masing-masing merupakan titik ujung dari masing-masing garis, yang termasuk ke dalam himpunan penyelesaian atau daerah yang diarsir. Pada soal, ditulis langsung apakah nilai yang dicari itu maksimum atau minimum. Biasanya, yang ditanyakan adalah keuntungan maksimum atau biaya minimum.

Contoh Soal

Soal 1: UN 2018
Untuk membuat 1 liter minuman jenis A diperlukan 2 kaleng soda dan 1 kaleng susu, sedangkan untuk membuat 1 liter minuman jenis B diperlukan 2 kaleng soda dan 3 kaleng susu. Tersedia 40 kaleng soda dan 30 kaleng susu. Jika 1 liter minuman jenis A dijual seharga Rp30.000,00 dan 1 liter minuman jenis B dijual seharga Rp50.000,00, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah ...

1. Rp500.000,00
2. Rp540.000,00
3. Rp600.000,00
4. Rp700.000,00
5. Rp720.000,00

Jika dibuat tabelnya, maka:

	Minuman A	Minuman B	Tersedia
Kaleng Soda	2	2	40
Kaleng Susu	1	3	30
Hasil Penjualan	30.000	50.000

Dengan memisalkan variabel x sebagai tiap liter minuman jenis A, dan y sebagai tiap liter minuman jenis B, dapat dibuat sistem pertidaksamaan berikut, serta fungsi objektifnya:
$\begin{cases} &x+3y\leq30 \\ &x+y\leq 20 \\ &x\geq 0\\ &y\geq 0\\ \end{cases}$
f(x,y) = 30.000x + 50.000y

Jika digambar grafiknya, maka grafiknya seperti berikut:

Daerah yang tertimpa warna merah dan hijau merupakan himpunan penyelesaian. Titik potong kedua garis juga harus dicari, karena termasuk dalam daerah himpunan. Titik potong dapat dicari melalui eliminasi kedua fungsi garis. Titik-titik yang akan diuji kedalam fungsi objektif tentunya adalah (0,10), (20,0) dan (15,5). Hasil akhir terbesar merupakan penyelesaian dari pertanyaan ini:

$\begin{align*} f(x,y)&=30.000x+50.000y \\ f(20,0)&=30.000(20)=600.000 \\ f(0,10)&=50.000(10)=500.000\\ f(15,5)&=30.000(15)+50.000(5)=450.000+250.000=700.000\\ \end{align*}$

Dari perhitungan dapat disimpulkan bahwa penjualan maksimumnya adalah Rp700.000,00.

Soal 2: UN 2018
Seorang petani memiliki lahan pertanian seluas 8 hektar. ia akan menanami lahan tersebut dengan tanaman padi dan jagung. Dari satu hektar tanaman padi dapat dipanen 3 ton padi, sedangkan dari satu hektar tanaman jagung dapat dipanen 4 ton jagung. Petani itu ingin memperoleh hasil panen tidak kurang dari 30 ton. Jika biaya menanam 1 hektar tanaman padi adalah Rp500.000,00 dan biaya menanam satu hektar tanaman jagung adalah Rp600.000,00, maka biaya minimum yang harus dikeluarkan petani adalah ...

1. Rp4.800.000,00
2. Rp4.700.000,00
3. Rp4.600.000,00
4. Rp4.500.000,00
5. Rp4.400.000,00

Jika dibuat tabelnya, maka:

	Lahan Padi	Lahan Jagung	Batas
Panen	3	4	30
Luas Lahan	1	1	8
Biaya	500.000	600.000

Dengan memisalkan variabel x sebagai tiap hektar lahan padi, dan y sebagai tiap hektar lahan luas, dapat dibuat sistem pertidaksamaan berikut, serta fungsi objektifnya:
$\begin{cases} &3x+4y\geq 30 \\ &x+y\leq 8 \\ &x\geq 0\\ &y\geq 0\\ \end{cases}\\$
f(x,y) = 500.000x + 600.000y

Jika digambar grafiknya, maka grafiknya seperti berikut:

Daerah yang tertimpa warna merah dan hijau merupakan himpunan penyelesaian. Titik potong kedua garis juga harus dicari, karena termasuk dalam daerah himpunan. Titik potong dapat dicari melalui eliminasi kedua fungsi garis. Titik-titik yang akan diuji kedalam fungsi objektif tentunya adalah (0,7.5), (0,8) dan (2,6). Hasil akhir terkecil merupakan penyelesaian dari pertanyaan ini:

$\begin{align*} f(x,y)&=500.000x+600.000y \\ f\left(0,\frac{15}{2}\right ) &=0+600.000\left(\frac{15}{2}\right )=4.500.000\\ f(0,8)&=0+600.000(8)=4.800.000\\ f(2,6)&=500.000(2)+600.000(6)=4.600.000\\ \end{align*}$

Dari perhitungan dapat disimpulkan bahwa biaya minimum yang dimaksud soal adalah Rp4.500.000,00.